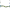by Jérémy Ribeiro

Entanglement may seem mysterious. It permits us to have correlations between two separate systems that are arbitrarily far from each other. Moreover these correlations are stronger than any (non causal) classical correlation we can think of. In some ways it looks like the two quantum systems can communicate between each other. This is why some people think that it might be possible to use it to devise an instantaneous communication system. I will try here to give you an intuition as to why this is not possible. But before we see why using only entanglement does not permit you to communicate, we have to understand what we really mean by ‘communicate’.

What is communication?

I don’t know about you, but each time my grandmother calls me, she asks me about the weather, so I’ll take this example to explain what I mean by ‘communication’.

So let’s imagine that you live quite far from your grandmother. We will assume that she is really smart and that she is locally all powerful (as are all grandmothers!). What I mean by that is that she is able to perform any calculation or operation (even quantum) very quickly and always knows what is the best operation to do in order to solve a problem. However she has “normal” access to information which comes sufficiently far from her place, for example she can get some information through the internet but she has no extraordinary powers to learn new information.

Now you and your extraordinarily smart grandmother will play a game. It will be a guessing game. She wants to guess what the weather is like at your place. The question is very open and there are many possible answers, so to make the analysis simpler we will simplify the game: she will try to guess whether it is sunny or not at your place. Then there are only two possible answers, “yes” or “no”, but what I will explain naturally generalizes to an open question too.

Now we will compare two possible scenarios for this game. In the first she tries to guess the answer without asking you anything (no communication). She might look on the internet to get an idea if it is sunny or not. However, as everyone knows that weather forecasts are not perfectly accurate, they can only give her the probability for each possible answer, and your grandmother will always guess the most likely one, and in our case, because there are only two possible answers, she will be right with a probability \( p_1 \geq \frac{1}{2}\) (we assume that \( p_1<1\) or else communication would be pointless).

In the second scenario, she will ask you for some information, and you must answer her honestly (honestly since you want to see whether or not you can communicate, so don’t confuse your grandmother!), saying \( 1\) for “yes” and \( 0 \) for “no”. Of course if she receives the answer perfectly it is easy for her to guess the correct answer with a probability \( p_2 \) equals to \( 1\). But if there is some noise in the communication channel you use she might only have partial information, and then \( p_2\) might be smaller than \( 1\). However, because your grandma is extremely smart, she knows how to best extract the maximum amount of information from what she receives, and then we must have that \( p_1 \leq p_2\). Indeed one thing she can do with what she receives is simply to ignore it, and then her probability of guessing the correct answer comes back to \( p_1\), so the best she can do with with that information is always better than just ignoring it, meaning that \( p_1 \leq p_2\).

Then we will say that there is some communication (between you and your grandmother) in scenario two if and only if \( p_1<p_2\). This therefore implies there is no communication if \( p_1=p_2\). An example in scenario two where there is no communication would be if you sent her the correct answer through a very noisy channel.

Can we build a communication channel out of entanglement only?

Now we will try to build a channel between you and your grandmother that uses only entanglement. As explained in the previous section, we will say that you succeed to send a message to your grandmother if her probability \( p_2\) that she guesses the correct answer is larger than the probability \( p_1\) that she guesses the correct answer when we know that there is no communication. So how can we build such a “channel”?

Scheme on the devices used between you and your grandmother. The measurements [latex] \mathcal{M}^{\theta}[/latex] and [latex] \mathcal{D} [/latex] are represented by the boxes.

For that look at the figure above. You and your grandmother share an arbitrary quantum system (for example two entangled photons, see my previous blog post or this video for more information) which can be entangled. In fact we won’t assume anything about this system (except that it obeys quantum mechanics of course). Finally we assume that you can share arbitrarily many entangled systems with your grandmother.

You encode the answer to your grandmother’s question “is it sunny?” in the variable \( {\theta}\). We will say that to answer “Yes” you set \( {\theta}=1\), and to answer “No” you set \( {\theta}=0\). Then the guessing game becomes, for your grandmother, trying to guess the value of \( {\theta}\).

To “send” her \( {\theta}\), you will perform a measurement \( \mathcal{M}^{\theta}\) on your part of the system. So for \( {\theta}=0\) you will perform a \( \mathcal{M}^0\) and for \( {\theta}=1\) you will perform another measurement \( \mathcal{M}^1\). These two measurements can be any of the measurements allowed by quantum mechanics. In fact allowing such general measurements is equivalent to allowing any of the quantum operations that quantum mechanics permits. It turns out that all quantum operations can be viewed as measurements. The difference is
that measurements give us some specific outcome. Here we will call the outcome \( x\) and we will assume for convenience that it is a bit (it could have been anything else but it is easier to explain like this), therefore \( x\) can take two values: \( 0\) or \( 1\).

On her side your grandmother will perform another measurement that we call \( \mathcal{D}\) on her part of the quantum system, and we will call her outcome \( z\). Again it can be any of the measurements allowed by quantum mechanics, and \( z\) will be your grandmother’s guesses for \( {\theta}\).

Also we let your grandma choose all the measurements \( \mathcal{M}^0, \mathcal{M}^1, \mathcal{D}\) and the state you will use, and because she is extremely smart she will choose the measurements and the state that maximize her probability \( p_2\) to guess the correct answer of the guessing game.

This example gives you all the power that quantum mechanics can give you in order to communicate only through entanglement. Now the
question is, can your grandmother use entanglement, and the very strong correlations it implies, to increase her guessing probability
and then have \( p_2 > p_1\)? The answer is in fact no, if we compute \( p_2\) then we find we always have \( p_2=p_1\) (Note: it is even very simple to prove, but unfortunately it requires that I introduce some mathematics which I won’t do here, but maybe in a future blog-post. Additionally the proof does not give a lot of intuition as to why it is impossible, it just says \( p_2=p_1\) and as a consequence that \( z\) is uncorrelated or independent of \( {\theta}\)).

This tells us that there is no communication possible between you and your grandma using only entanglement, but what about the quantum correlations? What happened? Indeed there exists some measurement such that \( x\) and \( z\) are strongly correlated, and so knowing \( z\) is gives you a lot of information about \( x\), so the “information” seems to go from your place to your grandmother’s place even if she lives on some planet around Proxima Centauri. So why are there no correlations between \( z\) and \( {\theta}\)?

To understand why this happens, I will introduce a distance \( D(A,B)\) that measures how correlated two random variables \( A\) and \( B\) are. For those who know a bit of information theory this distance is defined for all random variables \( A\) and \( B\) as \( D(A,B):=1-\frac{I(A,B)}{H(A,B)}\), where \( I(\cdot, \cdot)\) is the mutual information and \( H(\cdot,\cdot)\) is the Shannon entropy. For those who don’t know what a distance is, it’s a function of two objects which returns a positive number or zero. This number gives us an idea on how different the two objects are. Usually we use a distance in physical space, then the objects are points in space. In our case \( D\) takes random variables as the objects. There are then three fundamental properties about distances that I will define explicitly to make the following explanation easier:

1. Symmetry, meaning that for all \( A\) and \( B\), \( d(A,B)=d(B,A)\).
2. Positive definiteness, meaning that for all \( A\) and \( B\), \( d(A,B)\geq 0\) and \( d(A,B)=0\) if and only if \( A=B\).
3. Triangle inequality, meaning that for all \( A\), \( B\) and \( C\), \( d(A,B) \leq d(A,C)+d(C,B)\)

Triangle inequality. In a triangle, the distance between [latex] A[/latex] and [latex] B[/latex] is always smaller or equal to the sum of the distance between [latex] A[/latex] and [latex] C[/latex] and the distance between [latex] C[/latex] and [latex] B[/latex]

In our case, when the distance is \( D\), we can also add another property, namely:

4. For all random variables \( A\) and \( B\), \( D(A,B) \leq 1\). The equality case
\( D(A,B)=1\) being reached if and only if \( A\) and \( B\) are uncorrelated.

So let’s interpret what it means for two random variables to verify property \( 2\). If \( A\) and \( B\) are two random variables and \( D(A,B)=0\), then \( A = B\) meaning that \( A\) and \( B\) are perfectly correlated.

If I reformulate what I said previously in terms of this distance, then there exists some measurement such that \( D(x,z)\) is small (they are correlated) but in all cases \( D({\theta},z)=1\). Let me now use property \( 3\) to get \( D({\theta},z) \leq D({\theta},x) + D(x,z)\), and because \( D({\theta},z)=1\) we have:

\( 1 \leq D({\theta},x) + D(x,z)\)

Now we can see what happens with the correlations. If we use entanglement to have correlations between \( x\) and \( z\), then \( D(x,z)\) is small, and therefore we must have \( D({\theta},x)\) close to \( 1\) meaning that \( {\theta}\) and \( x\) must have very little correlation. On the other hand if we force \( {\theta}\) and \( x\) to be correlated, and we can force them to be equal, then \( D({\theta},x)=0\) and as a consequence we must have \( D(x,z)=1\) meaning that \( x\) and \( z\) are not correlated.

Note the inequality above does not only hold for quantum mechanics. It is true as long as there is no communication (i.e. the non-signalling condition), so it is true for classical correlation and even for correlations that would be stronger than quantum correlations.

To conclude, even if quantum mechanics permits us to have strong correlation at a distance it correlates only variables that are independent of what we input in the device we use. In other words, quantum mechanics can only correlate variables that are random, and on which we have no control. This means that the entangled systems you use do not carry any information since they ignore your input, and output – during the measurements – something random. If we try to control the outcomes, then the correlations between the two systems will disappear, and again no information has travelled. There is a trade-off between the correlations that you can have at a distance and the correlations between inputs and outputs of your measurement. As a consequence we cannot build a communication system that works only with entanglement.

Jérémy Ribeiro is a theorist at QuTech. He specialises in quantum cryptography: the use of quantum principles to design secure protocols for communication and other cryptographic tasks. In his free time (and sometimes during work hours) he enjoys practicing his Yo-yo skills and talking about open source software and undecidable problems.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.