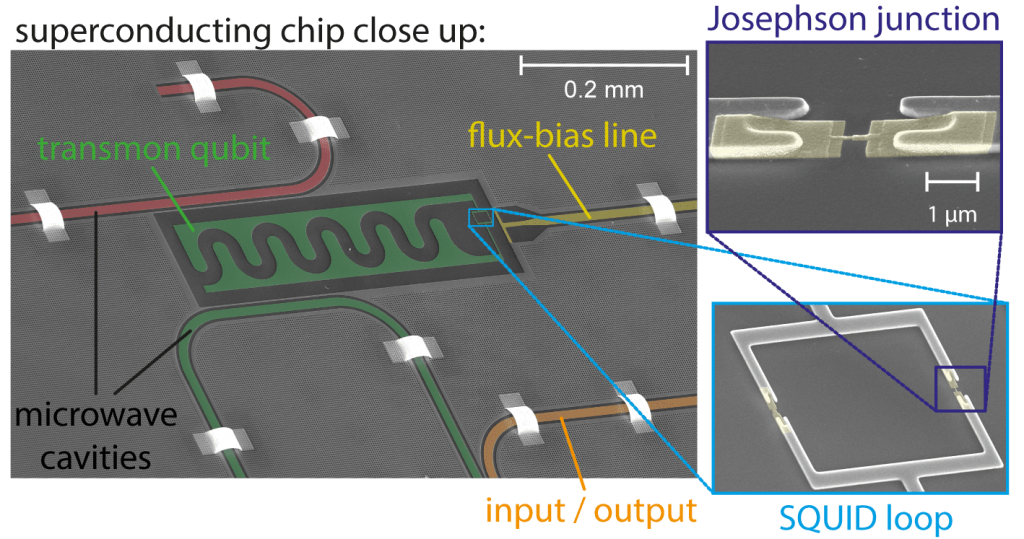
24.08.2017difficulty level - QQ
Hiding Schrodingers cat: a qubit of quantum error correction
by Tom O’Brien
If you’re reading a blog named ‘bits of quantum’, I guess I can assume you know a little bit about quantum computing and have a rough idea of what a qubit is. And, if you’ve read some of the previous articles on this blog, you may have gotten some idea of how difficult it is to make one. Being a quantum mechanic is real tough work, man!
Probably the largest challenge in quantum computing right now is minimizing the rate at which errors accumulate as you perform a computation on your quantum chip. In classical computers (your PC, or mobile phone), this is pretty much a solved problem. The probability of an error in any given operation is usually less than 1 in 1,000,000,000,000,000. This means in the process of me writing this blog post and it popping up on your screen probably less than one error has occurred. They’re not perfect, but after 50+ years of research and refinement, computers are pretty damn good these days.
Why error correct a quantum computer?
But quantum computers haven’t yet had 50+ years and tens of billions of dollars of R&D input. The state of the art quantum computers that make headlines (and ‘only’ cost millions of dollars) have error rates of about 1 in 1000. This mightn’t sound terrible (and honestly, it’s a considerable achievement to get this far), but quantum computation has a few additional caveats that amp up the trouble caused by errors:
1) Almost every single error in a quantum computation will ruin the entire algorithm. If I made a typo above, you could most likely still read this post (and you mightn’t even notice it!). But quantum algorithms are far more fragile, and any disturbance in the middle of the algorithm will usually result in the output being completely unrecognizeable.
2) The no-cloning theorem prevents backing up of quantum data. This theorem is famous in part due to its late discovery; the earliest-known proof comes from around the 1970’s, 50 years after the discovery of quantum mechanics. But the result is very strict; it is impossible to copy a quantum state, which implies that a quantum state has to survive on its own from start to finish during an algorithm.
3) Quantum computers are analog. You might have heard before of a qubit as a Schrodinger’s cat-on-a-chip, in a superposition of being alive and dead. But part of the power of a quantum computer is that it makes sense to talk not just about ‘alive and dead’, but ‘33.232% alive and 66.768% dead’. But if I sent you this cat across the internet, and while it was travelling it woke up a bit and became 33.233% alive, it would be very difficult for you to notice. Repeated small errors as we send our cat back and forth will then completely scramble our data, but at any single step we can’t tell that something has gone wrong.

As an aside, this ‘Chinese whispers’ or ‘death by a thousand cuts’ scenario is the reason why modern computers today are digital rather than analog. This is a bit of a shame; a perfect analog computer is far more powerful than a perfect digital one, but noise in the real world prevents us from having nice things.
4) Looking at a quantum state destroys the information contained within. Binary data can be fairly easily checked for errors with a checksum. This is a way of summing up individual digits to give a ‘0’ for any ‘valid’ data. Most credit cards have this feature, which allows online stores to detect common mistypings without needing to check your data with your bank (which is a nice security feature).
But, If I look directly at my cat in the example above not only do I either see it alive or dead, but the information about the 33.232% itself is lost forever (as this just told me the probability of seeing the cat alive when I looked). The same would happen if I looked at a ‘quantum credit card number’, destroying its usefulness. This information destruction (known as the Born rule) makes harnessing quantum computing in general very difficult. However, it turns out to also be our saviour from some of the problems above.
Hiding from errors in multiple boxes
To solve these issues, note the use of the word ‘directly’ in the previous paragraph. The key idea behind quantum error correction is to ‘selectively measure’ our quantum computer so that we hide the information we care about, both from us and from the errors that would destroy it otherwise.
As a theoretical physicist, it’s difficult to write the rest of this blog post without delving into the maths and scaring off anyone reading. But, I think I’ve found a nice example to at least give you a rough idea of how this ‘selective measurement’ works, as long as you note that this is a very simplified example, and you don’t mind more malicious cat abuse.
The idea is very simple: we hide Schrodinger’s cat in two boxes instead of one. Let’s label the boxes 1 and 2, and we hide the cat in the following way. If Schrodinger’s cat is in box 1 it is alive, but if it is in box 2, then it is dead. Using the previous numbers, our cat might be ‘33.232% (alive and in box 1), or 66.768% (dead and in box 2)’. Quantum mechanics has no problems with this (though an ethics committee might).

Although it is uncertain about which box the cat is in, and also uncertain about whether or not the cat is dead, we have prepared a system so that if the cat is in Box 1 it is definitely alive (green – a perfectly healthy colour for cats), but if the cat is in Box 2 it is definitely dead (red).
Then, I can ask a question about the state of the cat, without actually learning anything about the 33.232%. In particular, I can ask the (fairly long-winded) question:
‘Is my cat either (alive and in box 1) or (dead and in box 2)?’
Note that a ‘yes’ answer doesn’t tell me whether or not the cat is alive, nor does it tell me which box it is in. As such, I can safely preserve the 33.232% number no matter how many times I ask just this question. When I said ‘selective measurement’ above, I was thinking about questions like this, which only tell you a little bit of information about the system, and allow some reduced superposition to remain.
Ok, you might ask, so what? Well, let me imagine some error gremlin comes along while I’m not looking and changes the boxes. Then, the state of my cat would be ‘33.232% (alive and in box 2), or 66.768% (dead and in box 1)’. But now, if I asked my question again, the response would have changed to ‘no’. And, as long as the gremlin doesn’t look in the box itself, the 33.232% and 66.768% numbers are still preserved. So I can detect this error and correct it by re-swapping the boxes, and at all times I haven’t had to sacrifice my quantum information! Which ticks off issue (4) above.
It turns out that this trick deals with issue (3) as well. Suppose the gremlin was able to ‘just switch the boxes a little bit’, so now the alive cat has a little chance of being in box 2 (and the dead cat a little chance of being in box 1). When I make my measurement, and ask my question, I cause this superposition to collapse. The answer to my question must either be ‘yes’ (at which point no error has occurred), or ‘no’ (at which point a large, correctable error has occurred). This ability to turn small errors into either big errors or no error is the only reason that quantum computers can survive where analog classical computers cannot.
The problems putting theory into practice
Now, the main problem with the above example is that it doesn’t protect against most errors. For example, I have no protection against a malicious demon that just opens up one of my boxes and looks inside. In order to fix this, I need more cats, and more boxes. Or, because cats really don’t like sitting in the 10 millikelvin fridges that many quantum experiments are performed in, we need more cold, hard, qubits. But the general principle is the same as above. We combine multiple cold, hard, physical qubits by making these ‘selective measurements’ to make somewhat abstract ‘logical qubits’. And these logical qubits are unaffected by almost all the errors that we generally see in experimental systems.
Now, nothing in life is perfect, and this is definitely the case for experimental physics (oh snap, theoretical physics burn). Unfortunately, there will always be some errors that we can’t correct. But, these errors become very rare the more physical qubits we throw at the system. To go from the current 1 in 1000 error rate to a 1 in 1,000,000,000,000,000 error rate would take something around 200 physical qubits per logical qubit. 200:1 is a pretty bad ratio, but if it allows us to build a real quantum computer that can live up to the promises it has made so far, then we’ll do what we have to do.
As for where we are right now, in the next few months/years various groups have promised the first example of one of these ‘quantum error correcting codes’, including DiCarlolab here in QuTech. This will be a massive milestone on the road to a real quantum computer, so when you read somewhere that we have finally made and demonstrated such a device, you can be rightfully excited. But make sure to check that no cats were observed in the making of the chip.
About Tom O’Brien

Tom O’Brien
Tom is theoretically a PhD student from Leiden University, but he has been occasionally observed disrupting experiments in the DiCarlo lab by trying to model them. His interests lie mostly in designing new algorithms for quantum computers and trying to predict how well (or badly) they will actually work.