27.11.2020by Anne-Marije Zwerver
Entanglement and Bell inequalities
by Anne-Marije Zwerver
Bell inequalities
There is this rather peculiar habit that I have: I always wear earrings, but I make sure I never wear two earrings of the same colour. This has an interesting consequence: when you see me on the street and you notice that one of my earrings is red, you know with certainty, without looking, that the other one is not red. So, just by looking at the one earring, you gained information about the other. The earrings are somehow entangled. This could be puzzling for a little kid, that might ask: “How come that the earrings always decide to have different colour when they are looked at. How does the second earring know that someone observed the first earring and which colour it should be?”[1] You might be smiling and telling the kid that he overlooked something, an extra variable – hidden, if you want –, namely that I pick out my earrings with care in the morning and so determine their respective colours and even so their anti-correlation.
How random this example may seem, we could draw a comparison with quantum mechanics. All hell broke loose in physics around the 1920s, when physicists uncovered the laws of quantum mechanics, making predictions that baffle physicists still today. The laws of quantum mechanics brought rather counter-intuitive phenomena, such as superposition [see this blogpost], wave-particle duality [see this blogpost] and entanglement [see this blogpost], phenomena that seem to contravene basic physics principles, essentially reality and locality. With reality we mean to say that all objects have physical properties that are underlying a real physical state, regardless whether they are observed or not, and that these properties determine the outcome of a measurement. Or: when we’re not looking, the moon will still be there [2]. Locality, short for local causality, states that two spacelike separated objects cannot influence each other; causal influences cannot propagate faster than the speed of light.
In a superposition state, a particle (or wave if you want) is said to be in multiple states at the same time, but when this state is measured, it will pick one specific outcome. Such a state does not match with the concept of reality. Two entangled particles can be in an undetermined state, but when one of the particles is measured, the other particle will instantly be defined in a state (anti) correlated to the state of the first particle. These notions are extraordinary. How can they be explained in our local realistic world?
These concepts offered a breeding ground for many discussions on their interpretation. Many physicists racked their brains (and are still today). The most famous arguments came from Niels Bohr and Albert Einstein, considering the completeness of quantum theory and the consequences of its interpretation.
Especially entanglement was one of the points that bothered Einstein a lot. The idea that two particles could share a special, superluminous connection, went far against his ideas of physics. After all, it was Einstein himself who thought of special relativity and found out that nothing could go faster than light. How could these particles seem to violate this principle? To substantiate his point of view, Einstein, together with fellow scientists Podolsky and Rosen, wrote a paper titled “Can Quantum Mechanical Description be Considered Complete?” (the EPR paper) [3], in which they concluded the negative: it cannot. With curious consequences as non-locality, the rules of quantum mechanics are either wrong, or there must be a hidden variable that we don’t know about yet, but that explains quantum mechanics as a local realistic theory.
On the other side, as an anti-realist, Bohr had no problem with these new revelations of physics. In response, he wrote a paper as well, which he, ironically, gave the exact same title as EPR did and in which argued that no hidden variables were needed [4]. The discussion between Einstein and Bohr continued for years, as indicated by a letter that Einstein wrote to Max Born in 1947, in which he wrote:
“I cannot seriously believe in it [quantum mechanics] because the theory cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky action at a distance”. [5]
The EPR argument can be visualized by a variant of the argument put forward by David Bohm [6]. He proposed an experiment in which a source entangles two particles and sends these particles out in different directions. Both the particles can be measured along the z-axis and along the x-axis. Entanglement states that, when both the particles are measured along the same axis, their outcomes should be (anti-)correlated, whereas when they are measured along different axes, their outcomes should be random with respect to each other. Now, in quantum mechanics, we ask “How does the second particle know that someone observed the first particle and which outcome it should have, such that the particles are (anti-)correlated?”. But this is the exact argument that we laughed at before when the kid asked it about the earrings. For the earrings, there was a hidden variable underlying the correlations. Surely, something similar must happen in quantum mechanics. There must be a hidden variable that already determined the outcome of the entangled state for specific measurements and that guaranteed local realism to not be broken.
Bell inequalities in the classical world
But then, in 1964, John Bell published a paper, “On the Einstein Podolsky Rosen Paradox” in which he concluded that, if quantum mechanics holds, any description of nature cannot be local realistic [7]. Bell’s argument can be easily visualized. Let’s start with an example. In a room filled with people, I can ask everyone three yes/no questions:
- A: Do they wear glasses?
- B: Are they taller than 1.75 m?
- C: Do they have black hair?
Part of the people wears glasses, another part has black hair. Of course, there is also overlap; e.g. people with black hair and glasses, or tall people with black hair. We can divide the people over eight categories, as visualised in the Venn diagram below (categories are named Q – X).
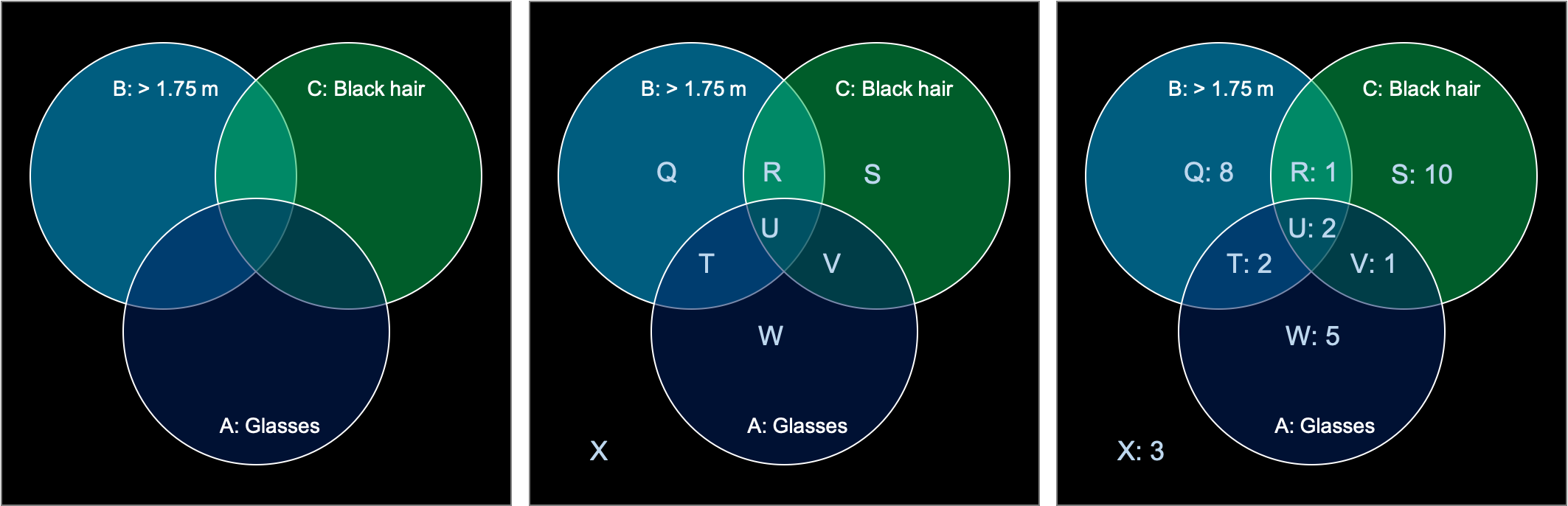
Now, the Bell inequality is the following. It states that the number of people that are in group A, but not in group B plus the number of people that are in group B, but not in group C is larger than, or equal to the number of people in group A that are not in group C.
So, in our case, the number of people who wear glasses, but are smaller than 1.75 m (Q +T) plus number of the people that are taller than 1.75 m, but do not have black hair (R+S) should be larger than, of equal to the number of people that wear glasses and do not have black hair (Q+R).
\(\begin{aligned} P(A\bar{B}) &+ P(B\bar{C}) &\geq& P(A\bar{C})\\ (Q+T) & + (R+S) &\geq& (Q+R)\end{aligned}\)
When we look closer at this inequality, we see that all areas on the right side of the equation, are also featured in the left side. So, the right side can never increase without the left side increasing as well. Therefore, the inequality must be true. And of course, the categories A, B and C could be anything. In a local, realistic world, this inequality will always hold.
Some photonics
So, let’s change the situation and look at a single photon that passes several polarizers: A, B and C, with different angles. But before we do that, let’s look a little bit into photonics. A photon has a polarization. This polarization can be horizontal (up/down), vertical (left/right), or a superposition of the two. When we send a horizontally polarized photon through a horizontal polarizer, the photon will always pass, whereas a vertically polarized photon will always be blocked by this polarizer. A photon that is approaching a polarizer with a 45-degree angle has a 50% chance of passing and a 50% chance to be blocked.
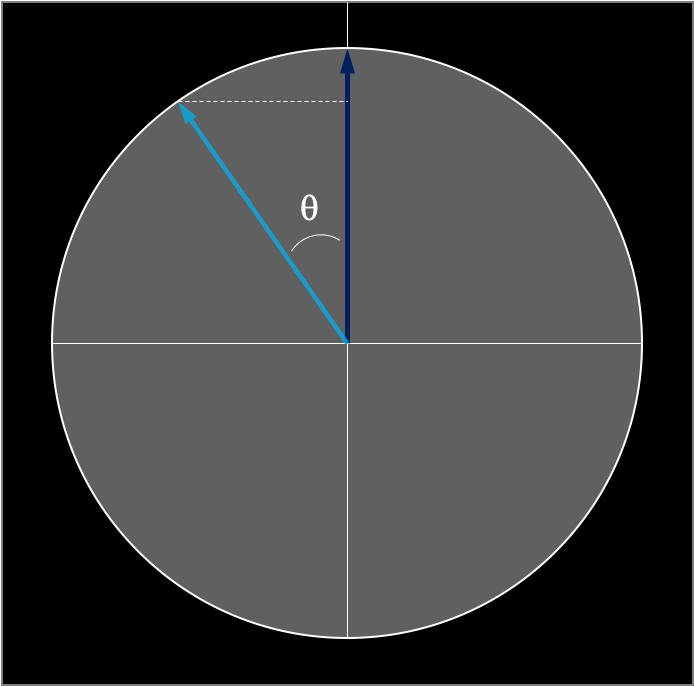
In general: the overlap that an incoming photon has with the direction of the polarizer will determine its probability of passing through. Thus, a photon that is oriented at an angle θ with respect to the polarizer, has a probability of cos2(θ) to pass and a probability of sin2(θ) to be blocked [8]. But, interestingly, after a photon passes a polarizer, it will be forced to take the orientation of the polarizer’s basis. We can see this as a quantum mechanical measurement, the photon ‘collapses’ in the direction of the polarizer.
Bell inequalities in the quantum world
If the quantum world is local realistic, as Einstein assumed, the quantum world should adhere to Bell’s inequalities. Let’s have a closer look at this using photons. We take three polarizers, again in three categories: polarizer A is directing upwards, polarizer B is rotated at an angle θ with respect to A and polarizer C is rotated with an angle 2θ with respect to A. We know that, for each polarizer, the photon will either pass, or be blocked, again these are yes/no questions:
- A: The photon passes A
- B: The photon passes B
- C: The photon passes C.
By sending a photon through two sequential polarizers, we can reproduce the inequality above: the number of photons that pass A, but are blocked by B plus the number of photons that pass B, but are blocked by C should be larger than, or equal to the number of photons passing A, but being blocked by C.
Let’s take this to the test. We shoot a photon with a random polarization down a path with polarizer A, so it has probability \(\frac{1}{2}\) of passing this polarizer. Thereafter, it has probability sin2(θ) of being blocked by polarizer B, polarized at an angle θ from A. So \(P(A\bar{B})=\frac{1}{2} \times \sin^2(\theta)\).
Since polarizer C is rotated at an angle θ from polarizer B, the probability that a randomly oriented photon that is sent to polarizers B and then C, passes B, but is blocked by C is also \(P(b\bar{c})=\frac{1}{2} \times \sin^2(\theta)\). Now, since polarizer C is rotated over an angle 2θ with respect to polarizer A, the probability of a randomly polarized photon first passing A (\(\frac{1}{2}\)) and then being blocked by C (sin2(2θ)) is \(\frac{1}{2}\sin^2(2\theta)\). Filling this in in our inequality, we get the following:
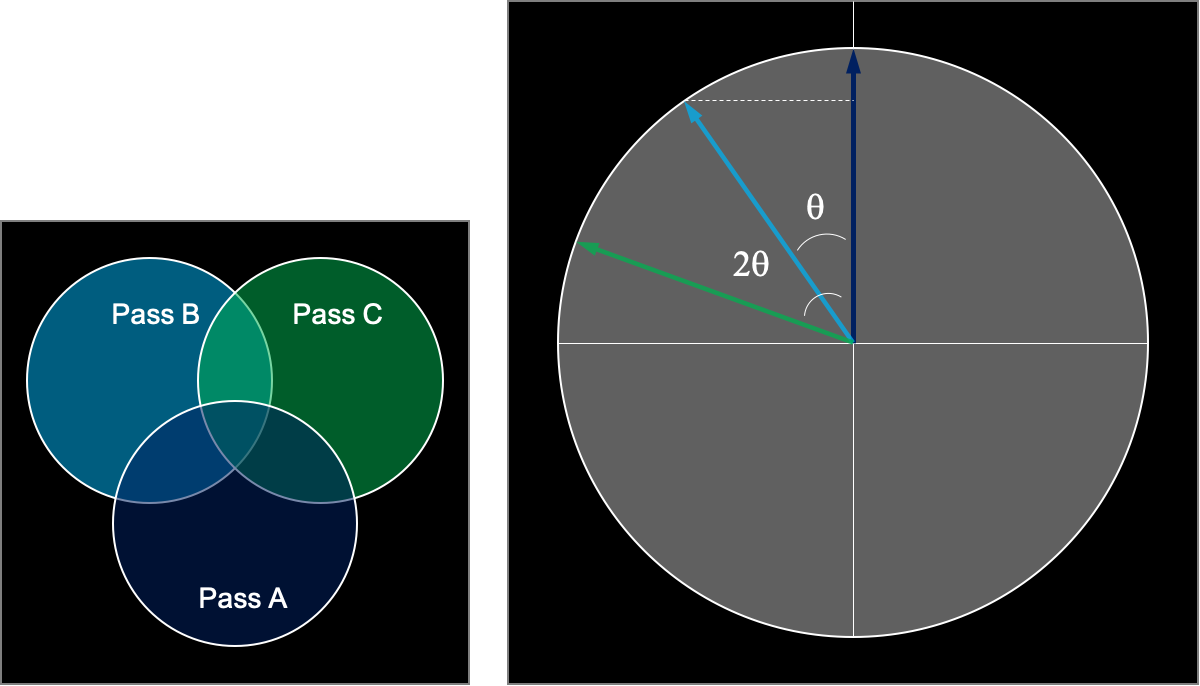
\(\begin{aligned} \frac{1}{2}\sin^2(\theta) + \frac{1}{2}\sin^2(\theta) &\geq& \frac{1}{2}\sin^2(2\theta)\\ \sin^2(\theta) &\geq& \frac{1}{2}\sin^2(2\theta).\end{aligned}\)
So according to the inequalities, sin2(θ) is always larger than, or equal to \(\frac{1}{2}\sin^2(2\theta)\).
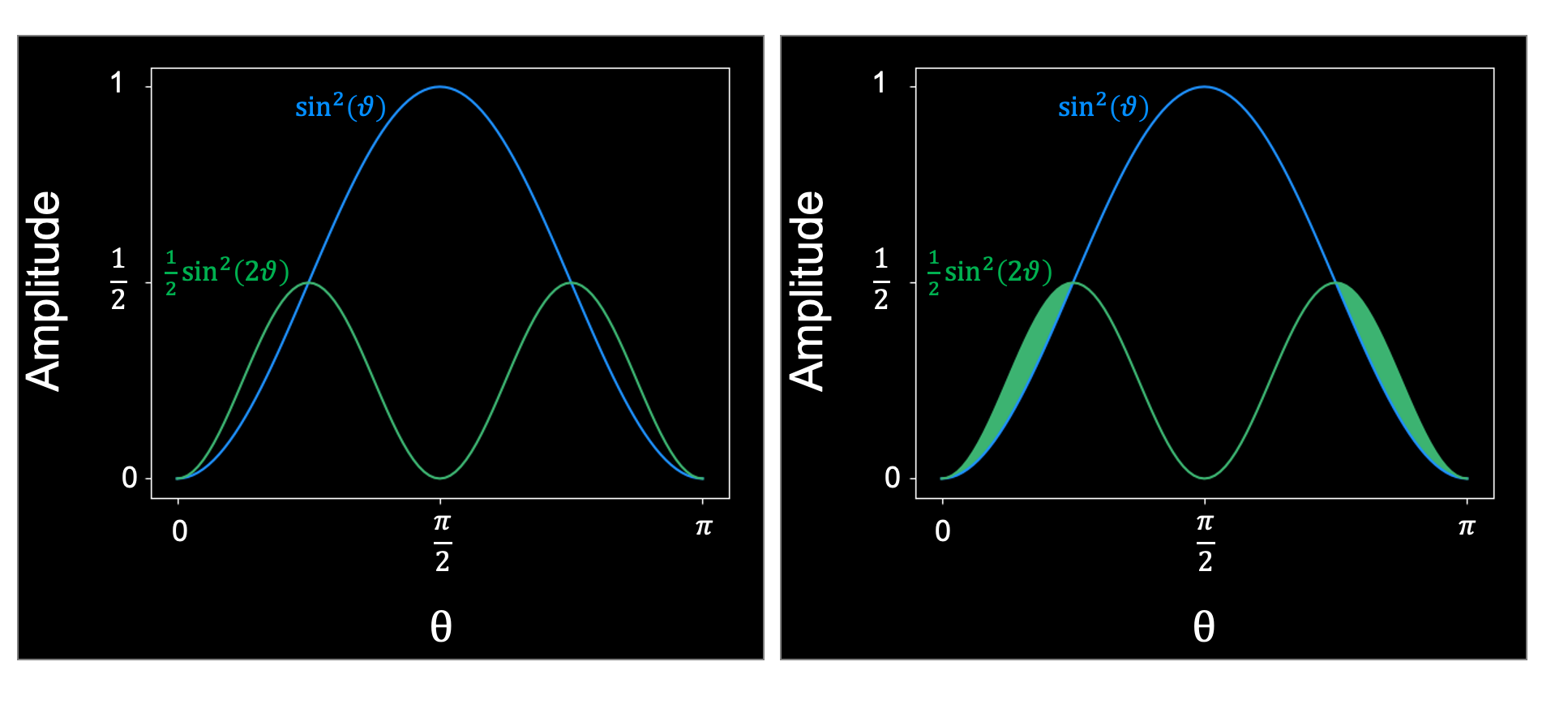
But when we plot these lines, we see that the inequality does not always hold, for example for \(\theta < \pi /4\). Wait, what?! But in a local realistic world this inequality has to hold. What happened? Well, actually it is pretty simple what happened: we cheated. How? Remember that we said that a photon going through a polarizer will, thereafter, be oriented in the direction of the polarizer. This means that, by going through polarizer A, we alter the photon, such that it suddenly possesses a different orientation with a different probability to pass B, irrespective of the initial probability to do so. The analogy of this effect in the Venn diagrams above is for someone to switch to a different group (e.g. by taking off their glasses) after we counted the people in category A. Okay, so our test was not completely fair. Let’s think of a better way to try and perform the second test.
Bell’s inequalities and entanglement
The fun thing is with quantum mechanics we can, by making use of entanglement. Let’s use the entangled pair
\( \frac{1}{\sqrt{2}} |00\rangle + |11\rangle \)With 0 being any random polarization and 1 being the orthogonal polarization. We know that these entangled photons that we send out are correlated when measured in the same basis, meaning that, when we measure one photon in ‘0’, the other photon will also always end up in the ‘0’-state. In order to not cheat, we send out these identical photons of an entangled pair and let one of the photons pass the first polarizer and send the other photon through the second. So, we study the probability of a photon passing A, while its counterpart is blocked by B, the probability of a photon passing B, while its counterpart is blocked by C and the probability of a photon passing A, while its counterpart is blocked by C. In this way, we should be able to test which photons belong in which group and recover the Bell-inequalities [9].
If ‘spooky action at a distance’ holds, entanglement should ‘collapse’ the second photon in the polarization of A, as soon as the first photon passes polarizer A (since sending a photon through a polarizer is some sort of measurement, so the first photon will ’collapse’ in the polarization of A and through the entanglement, so will the second). The second photon is now polarized in the orientation of A and the probability of the second photon passing B is thus, again, sin2(θ). This makes the probability of the first photon passing A, but the second photon not passing B again \(P(A\bar{B}) = \frac{1}{2}\sin^2(\theta)\). The same reasoning holds when we send the photons through polarizers B and C (\(P(B\bar{C}) = \frac{1}{2}\sin^2(\theta)\)), or through A and C (\(P(A\bar{C}) = \frac{1}{2} \sin^2(2\theta)\)). So also when we’re not cheating, Bell’s inequalities are violated in quantum mechanics, implying that entanglement is not a local realistic process. To properly do this test, we should ensure that the time between the first photon passing its polarizer and the second photon passing its polarizer is small. So small that the first photon cannot ‘cheat’ by quickly communicating its outcome to the second photon, such that the second photon can conveniently alter its orientation accordingly.
When Bell presented his theoretical violation of the inequalities, some physicists favoured to think that Bell took quantum theory too far; by using an argument ad absurdum, he just found the dark corners of the quantum mechanical theory, for how can the (quantum) world be not local realistic [10]? However, ever since Bell formulated his inequality, many experiments have been performed on violating Bell’s inequality. It took some years to get the experiments correct and ‘cheat-free’; the orientation of the polarizers had to be chosen randomly, the ‘fair sampling loophole’ had to be solved [11] and both the particles had to be measured before they had a chance to communicate. Nevertheless, all experiments demonstrated the violation of the Bell inequalities by quantum mechanics and in 2015, years after Bell first formulated the inequalities, the Bell inequalities were experimentally violated, loophole free [12, 13, 14]. Bell was proven right. This was big news, moreover mind-blowing: when photon 1 is measured, photon 2 instantly knows that this happened and will alter accordingly. Spooky action at a distance exists!
What does this mean?
What does this mean? Bell could think of four possible explanations. One of these was that the theory was not correct, which is now proven wrong by the experiments. So, we are left with three explanations that are all a bit puzzling [15].
Reject locality
Maybe, local causality does not hold. And these entangled particles do communicate faster than light. We shouldn’t be able to signal faster than light, though, because that would contradict the theory of relativity. But what does it mean that ‘we’ cannot signal faster than light? And can other species do so?
Reject reality
Another consequence could be that we have to give up our perspective of reality, at least in the quantum world. Meaning that particles can be in several places at the same time, or are basically ‘nowhere’ until you measure them. It is a bit like saying ‘is the moon there when nobody is watching?’.
Reject free will: Superdeterminism
The last explanation could be superdeterminism, meaning that photons already knew what questions they would be asked and how they would respond prior to the experiment. To be more precise, it would mean that everything would already be pre determined (and, thus, the rejection of free will) and that something, let’s call it the superdeterminer, would make fun of us by making us be puzzled about photon experiments.
For now, it’s up to you. Let yourself be amazed again as the little kid was about the earrings and reject (at least) one…
Literature
The cover image for this post is taken from [1].
[1] example adjusted from chapter 16 of J.S. Bell, “Speakable and Unspeakable in Quantum Mechanics”, Cambridge University Press, 1987 (version of 2004)
[2] D. Mermin, “Is the moon there when nobody looks? Reality and the quantum theory”, Phys. Today 38 (1985)
[3] A. Einstein, B. Podolsky, N. Rosen. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review, 47 (1935).
[4] N. Bohr, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review, 48 (1935)
[5] The letter was actually in German and the exact words he used were ‘Spukhafte Fernwirkung’
[6] Bohm, D. (1951). Quantum Theory, Prentice-Hall, Englewood Cliffs
[7] J. S. Bell, “On the Einstein-Podolsky-Rosen Paradox,”Physics 1, 195–200 (1964).
[8] Remind yourself that cos2(θ) + sin2(θ) = 1, so the photon will always either pass, or be blocked.
[9] The quantum part is based on: https://www.youtube.com/watch?v=8UxYKN1q5sI
[10] F. Laloe, “Do we really understand quantum mechanics?”, Cambridge University Press, 2012
[11] With the fair sampling loophole, you can cheat by not taking all photons into account, but, say, only taking photons into account that would pass test A.
[12] Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, Vol. 526, 682-686. 40.
[13] Shalm, L. K. et al. Strong Loophole-Free Test of Local Realism. Phys. Rev. Lett. 2015, Vol. 115, 1-10.39.
[14] Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, Vol. 115, 25040.38.
 Ever since she met Schrodinger’s cat, Anne-Marije has been fascinated by quantum mechanical phenomena. This brought her to QuTech where she is now playing around with qubits formed in semiconductor quantum dots. When not in the lab, she loves speed skating, running and wind surfing.
Ever since she met Schrodinger’s cat, Anne-Marije has been fascinated by quantum mechanical phenomena. This brought her to QuTech where she is now playing around with qubits formed in semiconductor quantum dots. When not in the lab, she loves speed skating, running and wind surfing.


