20.06.2019by Christophe Vuillot
Quantum Information Needs Protecting, and Here’s How to Do It
by Christophe Vuillot
Quantum physics is the strange and counterintuitive theory of physics governing the tiny world of atoms, electrons and photons. To access such small and ephemeral phenomena, scientists deploy advanced techniques to isolate and manipulate what can be destroyed by the tiniest breeze. Can they further protect these phenomena and make them survive to reach the scale of our life? This will be required to build a functional quantum computer.
Next time you go see a 3D movie, look at the screen of your smartphone through the 3D glasses [1]. Depending on whether you hold your phone vertically or horizontally, only one or the other lens lets the light through. This is because individual photons, the grains making up light, have a property called polarization which can be vertical or horizontal. Your phone screen happens to only produce one of these two types of photons and each lens of the 3D glasses acts as a filter, only letting through photons polarized in a particular direction. If you hold your phone diagonally, you see the screen through both lenses, but the light is dimmed. That’s because a diagonally polarized photon is in a quantum superposition of vertical and horizontal polarization. In practice, this means that such photons have an equal chance of being stopped or going through the lenses.
Now, for a real quantum experiment: hold your phone vertically and close the eye that can see the light emitted by the screen; so that you are now looking at a black screen. Pick a second pair of glasses and insert them diagonally just in front of the screen. Suddenly, you see something again; more light goes through! You have reproduced an equivalent of one of the first experiments which taught us that measuring quantum properties also modifies quantum states: the glasses you inserted diagonally measured the polarization of the photons in the diagonal basis which modified their state, such that some of the photons where now able to go through the second pair of glasses.

The experiment with the 3D glasses
Of course, your screen emits many photons at once, and to be fully convincing, your experiment would have to make photons go one by one. This makes everything considerably more difficult, but in labs around the world, scientists are getting so precise, they now routinely make experiments with single photons. They are capable of catching them inside mirror cages, looking at them without absorbing them and forcing them through interference experiments like yours one by one. This is not only true for photons: scientists around the world are also taming ions and electrons with unprecedented accuracy. So much so, they can orchestrate very complicated choreographies with multiple particles. This is still extremely challenging since the particles are not truly domesticated, and regularly disobey or even escape. But this endeavor is worth pursuing, since complex multi-particle dances are what a quantum computer would be made of. To understand what a quantum computer is and why scientists want to build it, we need to take a step back.
“Particles regularly disobey or even escape”
The development of quantum physics profoundly altered the way we envision how objects behave on microscopic scales. A new quantum revolution is now fundamentally changing how we describe information. Until now, information has been simply composed of bits: sequences of well-defined zeros and ones. Quantum information is different; it is represented by properties like polarization of photons – which can exist in superposition as you saw in the experiment. When you have a system in a quantum superposition (such as a diagonally polarized photon), using a polarization filter to measure whether it is horizontal or vertical yields a random answer. Furthermore, the state of the photon changes according to the answer. Another strange property of quantum information is entanglement, where two systems are strongly correlated for every measurement you can try on them. On top of that, quantum information cannot be copied: if someone hands you a quantum system and you do not know how it was prepared, you cannot make copies of it without modifying it. The energy state of single atoms or the spin of electrons are also viable properties to represent quantum information. All these systems share the fact that they are extremely small and therefore extremely challenging to manipulate and isolate from outside perturbations which explains their unruliness.
Despite all of its seemingly cumbersome properties, a closer study of quantum information has led researchers to the conclusion that some problems could be solved faster if one were to use quantum processing of quantum information; this is called quantum computing. For example, quantum computers would be able to factor very large numbers, simulate complicated molecules or solve some optimization problems, calculations that are impossible to do for a contemporary computer in a reasonable time. But, since a quantum computer uses such tiny elements, like photons, ions or electrons, as its building blocks, every little disturbance in its surroundings can change its state, leading to errors. It would seem that scientists need to almost completely eliminate disturbances coming from experimental imperfections and from the environment, in order to make a quantum computer work without errors. However, this is simply not possible. This is the problem that the field of quantum error correction aims to solve: How, using these noisy building blocks, can one still reliably process quantum information?
Quantum error correction
Error correction is already widely used nowadays: When you watch a video on the internet, or call your friends, the sound and image quality you experience is due to very efficient error correcting codes mitigating distortion and loss of information along the chain of transmission. Strikingly, one place where error correction is rarely used is your computer. This is because, while standard information can be altered in transmission, when you have all of it locally at hand, it is fairly robust. The zeros and ones in your computer memory so rarely switch by accident that no error correction is used in most computers. To understand why it is so robust, we have to take a closer look at what is it made of. The memory of your computer is made of integrated electronic circuits with transistors. In these circuits, a zero is represented by zero volts, and a one by usually 5 volts. These two states are distinguished by the flow of a plethora of electrons in the circuit. So, fluctuations of a few electrons are naturally corrected, since they are not significant enough to change a zero into a one. In a sense there is a built-in error correcting code which consists just in copying the information many times to ensure a correct interpretation.
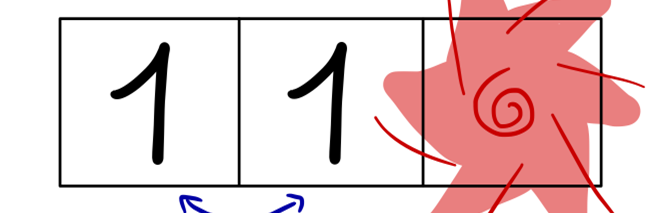
To conceptualize this error correcting code to its barest form, imagine you want to protect a single bit of information and you have three bits at your disposal. A particular error correcting code, called the repetition code works as follows: to encode the state ‘0’, put your three bits in the state ‘000’, and to encode the state ‘1’, put your three bits in the state ‘111’. Now if one of the bits is corrupted, for example you see the state ‘110’, then you know it must have been the state ‘1’ before corruption as there are more 1s than 0s left, this is called majority vote. Another way of looking at this code is to say that you have introduced correlations between the bits: when no error occurs, the first bit needs to be the same as the second bit and also the second bit needs to be the same as the third bit. When some corruption happens, this breaks the correlations. In the example the second bit is no longer the same as the third bit. The pattern of broken correlations actually tells you what happened to your system.

detecting one error with the repetition code
So now we stumble onto the first problem with quantum error correcting codes: we previously explained that quantum information cannot be copied and we also just explained that copying information is what makes standard information robust, so how are we going to make quantum information more robust?
“The potential future for quantum computers is looking brighter and brighter”
How is it that quantum information cannot be copied in the first place? You can think of quantum bits as impressionable toddlers playing a game of “what am I thinking”. They can think of an animal or a fruit and you are only allowed to ask them which fruit or which animal. The problem is that if you ask them “what fruit are you thinking of?” they will name a random fruit even if they where actually thinking of an animal to begin with. So without knowing if a toddler is thinking of a fruit or of an animal you cannot get more toddlers thinking of the same thing. But with this additional information you can make quantum copies. Back to photons and error correction: if someone hands you a photon and tells you that it is either vertically or horizontally polarized, you can measure it and produce a bunch of photons with the same polarization. So, by using a classical error correcting code, one can protect vertically and horizontally polarized photons. But how to deal with diagonally polarized photons? That is where we have to use entanglement. We said that when systems are entangled, they give correlated answers to the different measurements you can put them through. We also saw that error correction consists in introducing known correlations in the system. So, by using entanglement, it is actually possible to create quantum states which exhibit correlations in different basis and which act as error correcting codes in vertical, horizontal and diagonal polarization bases. Measuring these different correlation patterns in the different bases also gives information about what corruption might have happened, just like in the example above. This is the basic idea of quantum error correction.
Pulling this off in experiments is a real challenge, but it seems worth the effort. Once this technology becomes available, it will give us access to large and long-lived quantum systems. It is not only fundamentally exciting to be able to build such systems; they will also enable a whole new world of computation, from simulating complex quantum system to enabling quantum engineering, to solving math and optimization problems. The potential future for quantum computers is looking brighter and brighter.
[1] Some phones (like iphones) will not work since their screen produce different colors with different polarizations. Most computer screen would also work (but again not Apple’s). Also, some 3D glasses are not using vertical and horizontal polarization.
 Christophe Vuillot is a PhD in Barbara Terhal’s group studying the theory of quantum error correction and fault-tolerant implementations of quantum circuits. He particularly likes subjects with opportunities to draw pictures and once made a 3D movie as supplementary material of a paper. He enjoys good music, composes from time to time and tries to break free from Tech Giants by learning, implementing and promoting self-hosting.
Christophe Vuillot is a PhD in Barbara Terhal’s group studying the theory of quantum error correction and fault-tolerant implementations of quantum circuits. He particularly likes subjects with opportunities to draw pictures and once made a 3D movie as supplementary material of a paper. He enjoys good music, composes from time to time and tries to break free from Tech Giants by learning, implementing and promoting self-hosting.
Many thanks to Radha and Joel for their careful reading and feedback.