QuTech Blog – A blog from the people of QuTech

Bits of quantum

A blog from the people of QuTech

Authors

Subscribe to Blog via Email

Illustration of quantum information transmission

17.11.2022 by Remon Berrevoets

Do it safe, do it quantum!

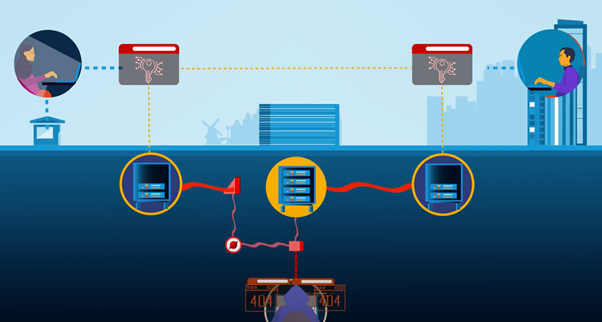
By Remon Berrevoets The future of encryption Encryption is all around us; from sending a WhatsApp message to securing digital bank transactions. Digital encryption is a way of making messages unrecognizable by scrambling them using a digital key, a list of zeros and ones. The scrambled message can only be decoded and read with ...

03.11.2022 by Valentin John

A Eurocrat’s guide to quantum computing

A Eurocrat’s guide to quantum computing by Valentin John Are you a Europhile or ...

21.04.2022 by David van Driel

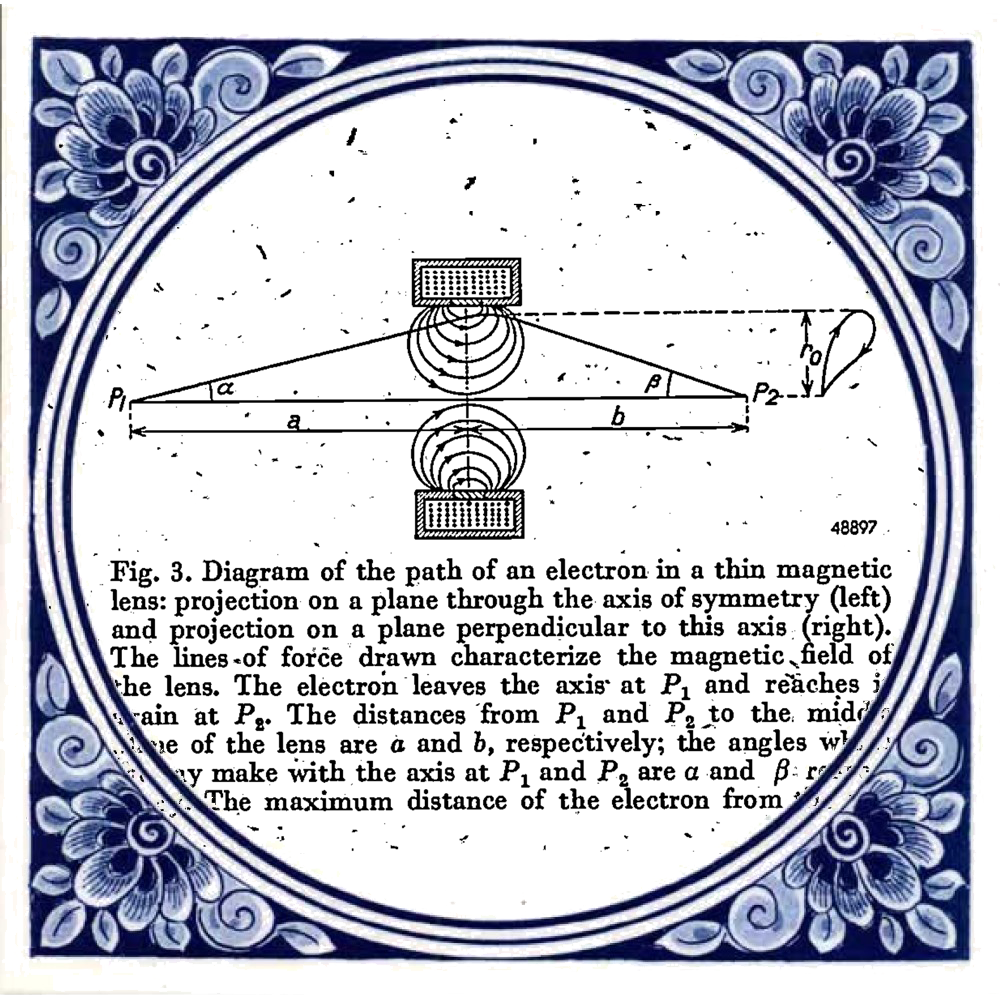
Van Keramiek tot Quantum/From Ceramics to Quantum Mechanics 2

Van Keramiek tot Quantum/From Ceramics to Quantum Mechanics 2 How Delft became the city ...

08.04.2022 Authors

March meeting-2022 experiences

APS March Meeting 2022 by QuTech blog editors With the first hybrid APS March ...

08.03.2022 by QuTech Blog Editors

"I didn’t know that we allowed whores in the lab"

I didn’t know that we allowed whores in the lab And more examples of being a woman in science. “Real change, enduring change, happens one step at a time.” ...

24.12.2021 Blog Editors

What type of QuTech qubit are you?

Which QuTech qubit type are you? by QuTech blog editors For those who have always wondered: find out which qubit type your personality fits best by responding to the ...

09.12.2021 by Sayr Motz

How to Support Your Trans Colleagues

How to Support Your Trans Colleagues by Sayr Motz Hello, my name is Sayr and I use they/them pronouns. I’m nonbinary, which means that I’m neither man nor woman ...

25.11.2021 by Aletta Meinsma

Goodbye to ‘quantum supremacy’?

Goodbye to ‘quantum supremacy’? by Aletta Meinsma On October, 2019, the news got picked up widely: “Google Claims a Quantum Breakthrough That Could Change Computing” headlined The New York ...

11.11.2021 by David van Driel

Van Keramiek tot Quantum/From Ceramics to Quantum Mechanics

by David van Driel Diagram taken from: H. A. Kramers and Helge Holst, The Atom and the Bohr Theory of its Structure (New York: Alfred A. Knopf, 1926) Tile ...

15.07.2021 by Pablo Cova Fariña

Analog quantum simulations with blue, big-eyed quantum dots

by Pablo Cova Fariña The world of quantum mechanics is quite a bizarre one. Take a bunch of particles, let them interact for a while and soon your computer ...

01.07.2021 by Christian Andersen

Where is the Rabi oscillation?

by Christian Andersen If you are an experimentalist and you want to check if you have a qubit in your experiment, then you may know that a good way ...

23.04.2021 by Tim Coopmans

How much GB do you need to back-up your quantum computer?

by Tim Coopmans A single quantum computer can be as powerful as a skyscraper-high pile of laptops – which is a curse for those designing it I work on ...